| |
返回
我們思考一下用一個、二個、三個和四個正方形相連組合,只有下圖九種情況:
阿隆‧拉扎勒斯就用29個小立方木塊做出了九塊這樣的立方體積木,考慮將這九塊立方體積木放到一塊
6X6 方格的棋盤版圖上,結果還餘七個空格,於是他以七個柱體 – 柱樁 (Blocker) 填滿棋盤;
不斷改變立方體積木的置法,七個柱樁位置也就對應改變。那麽將九塊立方體積木和七根木樁放到這 6X6 方格
棋盤版圖上有多種組合呢?通過電腦計算,找到 62208 種組合,並設計出七粒骰子來控制樁柱的置放。
棋盤版圖上的格子用座標表示,縱軸是 A、B、C、D、E、F,橫軸是 1、2、3、4、5、6。七粒骰子面上示出座標如下:
(1) A6, A6, A6, F1, F1, F1
(2) A5, A5, B6, E1, F2, F2
(3) A1, C1, D1, D2, E2, F3
(4) A4, B5, C5, C6, D6, F6
(5) A2, A3, B1, B2, B3, C2
(6) D5, E4, E5, E6, F4, F5
(7) B4, C3, C4, D3, D4, E3
我們發現上面骰子 (1) 和 (2)分別只有兩個和四個不同座標,如此 2X4X6X6X6X6X6 剛好是 62208 種柱樁的置法。
返回
二人玩法:
(1) 兩人各取一個棋盤、一套立方體積木和柱樁。
(2) 由一玩家同時將七粒骰子擲出,各人按骰子上的結果,將柱樁放在棋盤版圖相應的座標上。
6X6 方格棋盤版圖


按骰子擲出的結果,將柱樁放到棋盤版圖相應位置上
(3) 雙方都預備好後,比賽開始,二人要設法將這九塊立方體積木填滿棋盤版圖。
(4) 最快將棋盤版圖填滿者獲得勝利。
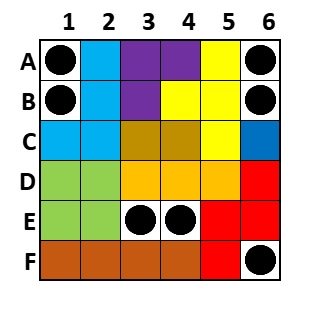
解答
一人玩法:
(1) 先取一個棋盤版圖、一套立方體積木和柱樁。
(2) 同時將七粒骰子擲出,然後按骰子上的結果,將柱樁放在棋盤版圖相應位置上。
(3) 設法將這九塊立方體積木填滿棋盤版圖。
(4) 當完成填滿棋盤版圖後,可以記下解答,移出這九塊立方體積木,從新嘗試將這些立方體積木去填滿棋盤版圖。
(5) 完成後又將解答記下。如此,盡可能找出多個解答。
筆名紅色標誌 (RedLogo) 的技術員和遊戲玩家用電腦程式對這遊戲骰子組合和解答進行分析,
在網上發表文章。在這 62208 個骰子組合中,每個組合都有解答,而組合的平均解答數是1936個,
組合中最少解答數是11個,最多是22317個。因此我們不要擔心這遊戲很難玩,絕對是適合家中老少同玩的。
西華盛頓大學 (Western Washington University, Department of Mathematics, Western CEDAR[註 1]) 的諾亞.詹森 (Noah Jensen)
也用電腦程式和群論 (Group Theory) 對這遊戲進行分析。在 8347680 (36C7) 個柱樁置法中,先除去那些沒有解答的置法,
例如留有兩個單立體和雙立體積木空間的置法是沒有解答的,而對稱的柱樁置法則合組尋找解答,如此可以減少電腦運算時間。
經過分析後,諾亞.詹森發現,有172440 個柱樁置法是沒有解答的。
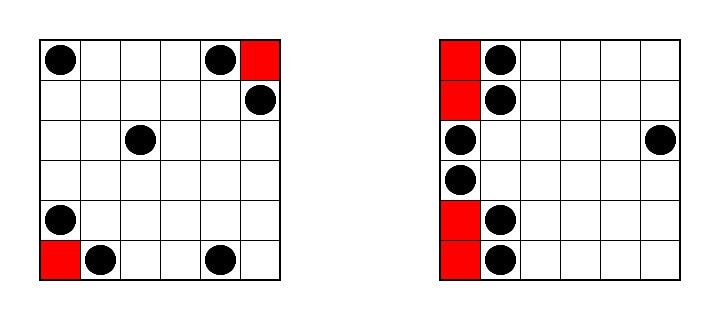
留有兩個單立體和雙立體積木空間的置法例子
諾亞.詹森也發現一個可以得出有解答柱樁置法的另一組骰子[註2]。
(1) A1, B2, C3, D4, E5, F6
(2) A2, B1, B3, C2, C4, C4
(3) D3, D5, E4, E6, F5, F5
(4) D1, E1, E2, F1, F2, F2
(5) A5, A6, B5, B6, C6, C6
(6) C1, D2, E3, F3, F4, F4
(7) A3, A4, B4, C5, D6, D6
我們如何判別柱樁置法座標圖形是否由〈機智方塊〉的七粒骰子而來?當然我們可以核對柱樁座標是否來自這七枚骰子,
逐一檢查座標,這較花時間。我發覺諾亞.詹森將同骰子面上座標用同顏色塗在 6X6 格子的色區圖很有用,
它可以幫助我們輕鬆地作出判別 – 只要柱樁圖形上七個柱樁座標都在不同色區內,就是〈機智方塊〉的柱樁置法,有解答;
反之,若有兩個或多個座標落在同一色區內,那就不是〈機智方塊〉的柱樁置法圖,就不保證有解答。
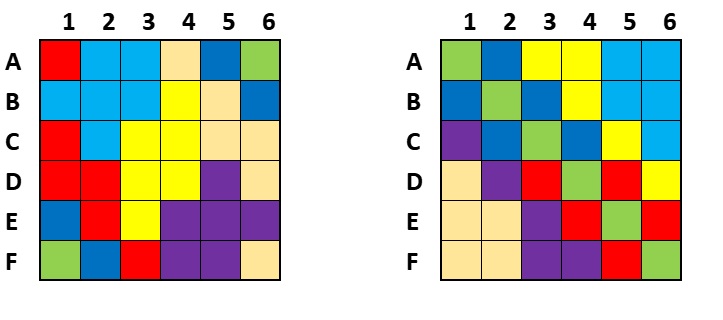
〈機智方塊〉和諾亞.詹森的骰子色區圖

有兩個柱樁座標在同一色區內,不保證有解答
上面例子的柱樁置法可能沒有解答,因為骰子 (A4, B5, C5, C6, D6, F6) 被重複,
骰子 ( A5, A5, B6, E1, F2, F2) 被代替了。
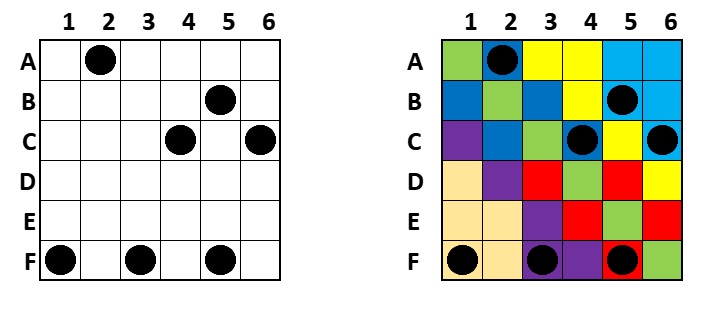
用諾亞.詹森骰子色區圖來判別,也是不保證有解答

用木小立方體粒自製〈機智方塊〉
[註1] DEDAR 是 “Contributing to Education through Digital Access to Research” 的縮寫。
[註2] 這組骰子能得 93750 (5X5X5X5X5X5X6) 個有解答的柱樁置法。
參考資料
|
|