1820年法國出版了一本與當時的遊戲書完全不一樣的《法國新拼板遊戲（Neuveau Casse-tête français）》，
不僅圖形新穎，並且還在圖形上添加色彩，使得那些圖形看來就像一幅活潑生動的畫。
在十九世紀下半葉以前，法國、德國及荷蘭都以七巧板作為一種純粹的拼圖遊戲，大約到了1860年，七巧板遊戲漸成了主導，
也被改成今天的板塊狀形式。1818年這遊戲還是以書本的形式來介紹，現在已是將板塊放在盒子裏，圖和解說就印在卡片上出售。
到了十九世紀末和二十世紀初，兩位遊戲專家也是七巧板狅熱愛好者把他們的全部精力都投入於對這遊戲的探索：
有1903年山姆．洛伊德（Sam Loyd）的書《唐第八卷書之第一部（The Eighth Book of Tan Part I）》和亨利．歐內斯特．杜德尼
（Henry Ernest Dudeney）在《河濱雜誌（The Strand Magazine）》1908年11月號卷 XXXVI （No.215 p581–p585）
的謎題專欄文章〈七巧板的故事（Tales with Tangrams）〉。洛伊德為七巧圖提供了許多自創的新圖形，在《唐第八卷書之第一部》
他提到中國人李洪章（Li Hung Chang）曾說過：「孔子創造很多有關七巧板的典故，七巧板是兒童認物認形，青年們鍛練智慧，
成年人學習數學，藝術家獲得設計，詩人啟發靈感，讓人明智思考過去、現在和未來的遊戲。」
近年在這方面出版的書籍，直接或間接都依靠洛伊德和杜德尼的工作。當多佛出版公司（ Dover Publications Inc.）
於1968年出版洛伊德的《唐第八卷書之第一部》書後，英國《數學公報（The Mathematical Gazette）》
（ Volume 54 Issue 387 February 1970 p80） 也把這書介紹給教師們。
洛伊德在書中也提出一個七巧板創於四千年前之說，七巧圖用金字書寫在羊皮紙（printed in gold-leaf upon parchment）上。
在《唐第八卷書之第一部》出版後，一躍而成為謎題界的經典之作，連杜德尼也以為洛伊德的「四千年說」為真，
以至在他的文章和出版的書中經常提及，例如上面介紹的雜誌、《數學娛樂（Amusements in Mathematics）》和
《老式具挑戰性謎題（Good Old Fashioned Challenging Puzzles）》。如此再經過杜德尼這專家宣傳，
就使得洛伊德的「四千年說」人皆盡知，連美國著名謎題專家馬丁．加納德也在他的《第二輯數學謎題
（The Second Book of Mathematical Puzzles and Diversion）》（ p210–p214） 一篇文章〈機械拼圖（Mechanical Puzzles）〉
說七巧板是幾千年來的一款東方消遺玩意。
看來「四千年說」似是定論，但近來己有所改變。先是羅納德． C．里德（Ronald C. Reed） 在他的書
《七巧板330拼圖（Tangrams 330 Puzzles）》 中指出「在公元前2000年，中國人還處於文學成就主要是以粗糙象形文字刻於龜甲上的階段，
他們甚至沒有進步到可以在細竹條上書寫 - 例如，像儒家經典最初的記錄方式（大約公元前500年）
（In 2000 B.C. the Chinese were still at the stage in which their literary achievements mainly consisted of crude pictographs scratched on tortoise shells;
they had certainly not progressed even to writing on thin strips of bamboo -
the way in which Confucian classics, for example, were originally recorded （around 500 B.C.））」。
當然里德的說法是正確的。大家想想，從幾千年前至今的中國是把文字刻寫在銅器、龜甲、竹簡、木册、絹帛和紙上，
根本沒有以羊皮紙金字的書籍。加納德在《科學》（Scientific American August 1974 Vol231 No.2 p98–p103B）
專欄中收回「七巧板是幾千年來的一款東方消遺玩意」的說法（In this department for September, 1959,
I called tangrams the oldest of dissection games and said that the Chinese had been amusing themselves with it for several thousand years. This is totally wrong.），
杜德尼的「四千年說」是純粹自製的傳說。加納德這篇文章也收錄在他的《時間旅行和其他數學困惑
（Time Travel and Other Mathematical Bewilderments）》書中。
劉易斯．卡羅爾（Lewis Carroll） 在自己的藏書中也有一本書《時尚中國謎題（The Fashionable Chinese Puzzle）》，
也與費城版的七巧板書相似。英國遊戲專家杜德尼後來知悉這書，認為七巧板是拿破倫（Napoleon）在被放逐聖赫勒拿
（St Helena）時每天花幾小時來鍛練耐性和腦力的遊戲。費城版書本內都有這述說，但並不表示這真有其事，
因為拿破倫在他的自傳中只提及他在流放時興趣於桌球、棋和翻轉棋（ reversi 或黑白棋），沒有說到拼七巧圖。
雖然如此，我們不能否定拿破倫有玩七巧圖。
七巧圖傳到歐美國家後都受到重視。《美國教育雜誌（The American Journal of Education）》1859年3月–6月號卷VI No. XVI–No.XVII p.452
的文章認為七巧板可作為幾何教育的教具，推薦給四歲至十二歲的兒童，先從簡單幾塊三角板續步增加至全部七巧板塊，依著七巧圖形，
拼出解答，訓練兒童的觀察、分析和圖形切割能力。
美國雜誌《伊利諾伊州教師（Illinois Teacher ）》（編輯S. A. Briggs, 芝加哥Chicago）1864年8月號卷10的一篇文章對
「Tangram」這詞作闡釋，並介紹七巧圖。
大約在1818年當精美的七巧板拼圖傳到丹麥和兩本有關書籍的出版後，七巧板遊戲也就流行起來。
一名哥本哈根大學的學生寫了一本關於中國遊戲的歷史和流行的書，人們對這七巧圖謎題的興趣猛增。
另一本書《新中國遊戲（Det nye chinesiske Gaadespil）》包含《唐第八卷書之第一部》書中的339個七巧圖形，
也有助於七巧板在丹麥的普及。
在德國，七巧板的流行較晚一點，主要是翻譯中國傳入的《七巧圖合璧》。1981年工業家弗雷德克．阿道夫．里希特（Friedrich Adolf Richter）
給德國民眾介紹七巧板，他稱這遊戲「錨拼圖（Anchor Puzzle）」，人們用石或陶來製造七巧板。
益智圖發明以後，風靡一時，不僅在十九世紀末傳到海外，還出版了相關書籍，當時被稱為「十五塊魔術積木（fifteen magic blocks）」。
人們認為用這些「積木」不僅可以拼出各種器物、用品、人物，它也可作為幾何教育的輔助教具。
1901年伊薩克．泰勒．海德蘭（Issac Taylor Headland）著的《中國男孩和女孩（The Chinese boy and girl）》書中有一章節
〈積木遊戲 – 幼稚園（Block games - Kindergarten）〉講述作者和一位在玩十五巧板的學童的互動，
他拼出很多與中國文學有關的事件和人物的益智圖形，夾在文字間，篇排得很特別。
《中國男孩和女孩》書封面和〈積木遊戲 – 幼稚園〉章節部分
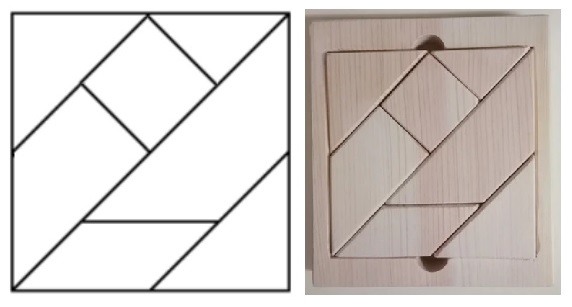
清少納言智慧板
清少納言智慧板的圖形切割法
大家可以用紙板按上圖的切割法或
摺紙，做出一副清少納言智慧板來玩。
下面是清少納言智慧板圖形例子，請用自己做的清少納言智慧板拼出解答：
《雜藝叢書》（日本大正 4年二月 1915年）的〈清少納言智惠の板序〉中寫道︰「記清少納言，見古書，多見富於智慧，使人心愉快之事，
其中，有命名為智慧之板，表現圖之智慧卷（清少納言の記せる古き書を見侍るに、智ふかくして人の心目をよろこばしむること多し、
其中に智恵の板と名づけ、圖をあらはせるひとつの巻あり）」，下款題「寛保二年戌八月 含靈軒述」，所以大家就認為是含靈軒所著。
《清少納言智惠の板》序（手寫） – 含靈軒
《雜藝叢書》–〈清少納言智惠の板序〉
日本數學家平山諦（Akira Hirayama）在他的著作《東西數學物語》亦寫道：
| |
寛保2年（1742年） 有一個以「含靈軒」的匿名寫了一本小册子，書中說：「記清少納言，見古書，多見富於智慧，使人心愉快之事，
其中，有命名為智慧之板，表現圖之智慧卷，當閱讀此書時，幼稚兒女，因智之深淺，自然取萬物之形，作各種器物之圖，確為微妙也。
雖則，其圖為往昔之器物之形，又為靈上御持之物，故今日之兒女不知其心，故，重新複製其圖之器物，記其近似之形。」
（見《東西數學物語》平山諦著 代欽譯 上海教育出版社 2005, 恒星社昭和53年增補2版 p202）。
|
不過平山諦認為《 清少納言智慧板》的真正作者是環中仙（ Kanchusen）。 環中仙生殁不詳，是活躍於享保年間的人士，而且當時以環中仙、
多賀谷環中仙（Tagaya Kanchusen）、環中仙元陳（Kanchusen Genchen ）和 環中仙伊三（Kanchusen Isan） 不同名義，著作多本數學書，
因此平山諦有這種推測。
這些著作內容涉及數學、數學遊戲和魔術等範疇：
《初心算法早傳授》上、下、加 – 共3卷 環中仙撰 享保11年正月（1726年）
《初心計算法早傳授》卷上
《和國智惠較》（或《和國智惠角力》或《和國智惠角方》） 2 卷 環中仙撰（享保 12 年，1727 年）
《和國智惠較》
《珍術さんげ袋》2卷 環中仙い三撰 享保10 年左右（1725年）
《珍術さんげ袋》序 環中仙い三
《続さんげ袋》 2 卷 多賀谷環中仙撰 明和元年（1764年）11月
《唐士秘事海》 2 卷 多賀谷環中仙撰 享保18年（1733年）
《唐士秘事海》序 多賀谷環中仙
《璣訓蒙鑑草》3卷 多賀谷環中仙撰 享保15年（1730年）
《璣訓蒙鑑草》序 環中仙
下圖是《璣訓蒙鑑草》梅卷末尾的廣告，有兩頁，可見環中仙的書大部分都是含靈軒出版的。平山諦認為是因為被環中仙選中，
才以含靈軒的名義出版的。它缺乏決定性因素，但似乎很有可能。
《璣訓蒙鑑草》 – 梅卷末載含靈軒發行書刊目錄廣告 享保15年（1730年）
寬保三年癸亥（1743年）中根彥循的《勘者御伽雙紙》，是本數學遊戲書。
《勘者御伽雙紙》序
《勘者御伽雙紙》卷上第十八章〈裁合物の事〉有一個圖形分割和重組問題：豎劍將一個1：2的長方形分割成6塊，
可重組出正方形、三角形、梯形和其他形狀。其中的鱗片形狀、袴腰（腰板）和拔釘器在名稱和形狀上與
《清少納言智惠の板》書中的名稱和形狀非常相似。
《勘者御伽雙紙》第十八章〈裁合物の事〉
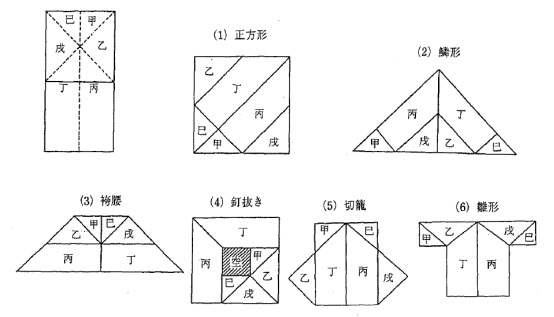
《勘者御伽雙紙》〈裁合物の事〉章的圖形分割組合問題
在那時期，將圖形分割重組，是數學遊戲內容之一。
清少納言智慧板拼出正方形的方法有二，也可拼出中空的正方形（釘貫），這與七巧板只能拼出一個正方形和不能拼出中空的正方形不同之處。
另外題為「鱗形」中空直角等腰三角形，原書繪畫完美，但在實際嘗試時，底部中央有突出部分。有關類似錯誤情況的圖形也不少，
例如問題中的「蓮花」圖，實際組合時花與萼並不貼合，不像書中給出的解答那般完整接合，細微處被忽略了；
「神鏡」在問題中是八角形而在解答是六角形，且鏡柄也較長；還有「鴛鴦」的臉型在問題和解答裏是不同的。
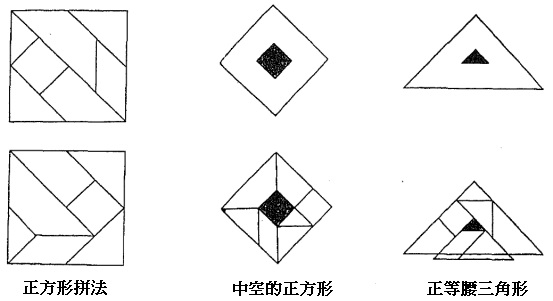
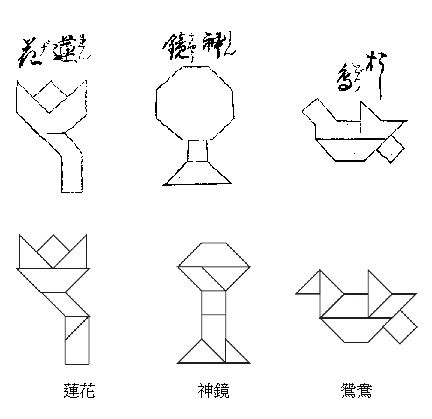
圖「蓮花」、「神鏡」、「鴛鴦」和解答
從一些文獻記載中，可以了解到清少納言智慧板在被發明後，也成了當時民間婦女和兒童們的流行玩具。
在齋藤幸成的《武江年表》記錄了延享年間（1744年–1747年）的事，「智慧板 – 即使是現在，它也是一個供孩子們玩耍的板子。
（智惠筏（ちゑいかだ） – 今も子供のもて遊ぷちゑの板なり）」平山諦：「智慧笩，今日之兒童遊戲，為七巧板也。」
（見《東西數學物語》 平山諦 代欽譯上海教育出版社 2005, 恒星社昭和53年增補2版）
《武江年表》
明治41年（1908年）的《古事類苑》（1262頁）亦有清少納言智慧板是兒童玩具，也是作為禮物送給兒子的記載。
在「智惠板」節有兩段引自《大江俊矩記》和《武江年表五》的記述：
| 《大江俊矩記》記述1804年時有一個人將智慧板作為新年禮物送給兒子。 |
| |
《大江俊矩記》享和四年（文化元年，1804年）正月六日丙申，美濃屋伊介，年玉絹糸一包、子供兩人へ手遊、智惠板一箱、將棊盤一箱。
（享和四年（文化元年，1804年）正月六日丙申，美濃屋伊介，將新年禮物絹系一包、智慧板一箱、將棋一箱，給兩個兒子玩。）
|
| 《武江年表五》記載延享二年江戶流行俳句集《時津風》和智惠板。 |
| |
《武江年表五》此年間（延享）記事 – 延享二年の 春，江戶の流行物を集めたる句集あり、時津風と題す、時々
庵門人反故齋果然といへる人の編也，畫は寄合書きなリ其內を撰て目次のみを左にゑるす、中略。
智惠笩（ちゑいかだ） – 今も子供のもて遊ぷちゑの板なり。
（記此年（延享）之事 – 延享二年春，曾有過江戶流行事物俳句集，題目為《時津風》，
時時庵門人名叫反故齋果然的人所編寫，撰寫者僅寫出目錄放在左側。智慧板，即使是現在，
也是一個供孩子們玩耍的板子。）
|
《古事類苑》（1262頁）
《俳諧時津風》 – 圖取自〈清少納言知惠の板〉《數學史研究》1999年7–9月
在那之後，似乎在明治時代臨近之前一直享受著的「清少納言智慧板」，它似乎也在明治時代繼續存在，
這是因為它也出現在樋口一葉於明治28年（1895年）12月寫的小說〈青梅竹馬（たけくらべ）〉中：
「他要是不来，我也不高興先玩幻燈了。伯母，你們鋪子裡有智慧板賣没有？老虎棋也行，甚麽都行，老閑着真無聊！」美登利說。
（彼の人が来なければ幻燈をはじめるのも嫌、伯母さん此處の家に智慧の板は賣りませぬか、
十六武蔵でも何でもよい、手が閑で困ると美登利の淋しがれば）
《一葉全集》 樋口一葉〈青梅竹馬〉５章（明治28年）
昭和3年2月（1928年）浪速叢書第五的《攝陽奇觀(五)》 卷42謂先前是以清少納言智慧板拼出人物花鳥器財等，
到寛政年間（1789年–1800年）就用新製作的十九枚智慧板來拼出圖形。下圖是《攝陽奇観(五)》 卷42第59頁，
是清少納言智慧板和38個圖形解答，大部分與《清少納言智慧板》相同，但有些在名稱上有變化，
形狀或組裝方式也不一樣。第60頁是當時新發明的十九枚智慧板。
《攝陽奇觀(五)》 卷42 p59–60
十九枚智慧板圖形
十九枚智慧板 – 《智恵乃いた （ちえのいた）》 新日本古典籍總合データベース
江戶時代後期（約1780年），浮世繪師喜多川歌麿（Kitagawa Utamaro）的畫作〈角玉屋内 誰袖 きくの しめの〉描繪了兩位女士在玩拼板圖，
細看之下，似乎是玩十九枚智慧板，這說明智慧板在當時是十分流行的。
喜多川歌麿的畫作〈角玉屋内 誰袖 きくの しめの〉
〈睡道人序〉–《七巧圖合璧》
其後清光緒四年戊寅（1878年）重刻同治元年（1862年）版童叶庚《益智圖》上、下卷，商務印書館民國六年丁巳（1917年）
重印光緒十五年己丑（1889年）版童叶庚《益智燕几圖》、《益智燕几圖副本》（即《益智燕几圖》解答）、
光緒四年戊寅（1878年）版童叶庚《益智圖》上、下卷、光緒六年庚辰（1880年）版童昶、童昂、童晏《益智續圖》上、下卷，
民國七年戊午（1918年）重印光緒二十四年戊戌（1898年）版《益智圖千字文》八册等書籍，都傳到日本。
七巧板傳到日本後，也在兒童婦女間流行起來，受到教育界的重視，亦有人重編有關七巧圖的書籍，亦有在編寫遊戲書籍時，
將七巧板與清少納言智慧板、十九枚智慧板一同收納書中。
明治28年2月（1895年）寸舟漁史編奥沢信行發行的《教育遊戯七巧板》，是本七巧圖書籍，繪列的七巧圖形多取自《七巧圖合璧》，
未附解答，以待玩者尋找。捉雲道人的〈序〉中云：「兒童之ラ學業ノ餘暇ニ玩ンカ其開智通理。」
〈序〉捉雲道人 – 《教育遊戯七巧板》
《教育遊戯七巧板》
七巧板是分割組合玩具，有教育的意義。明治18年乙酉（1885年）飯島半十郎編纂了《幼稚智恵のみちひき》兩卷，
上卷對七巧板的製作和幾何特性作詳細分析，並分類繪列圖形，有幾何圖形、魚獸、諸鳥、器具、家屋橋樑、船艦、
人物、數字和英文字母圖形；下卷是圖形的解答。《幼稚智恵のみちひき》一書也收錄在昭和52年（1977年）
《明治保育文獻集》第四卷中。
《幼稚智恵のみちひき》上卷–序和圖式
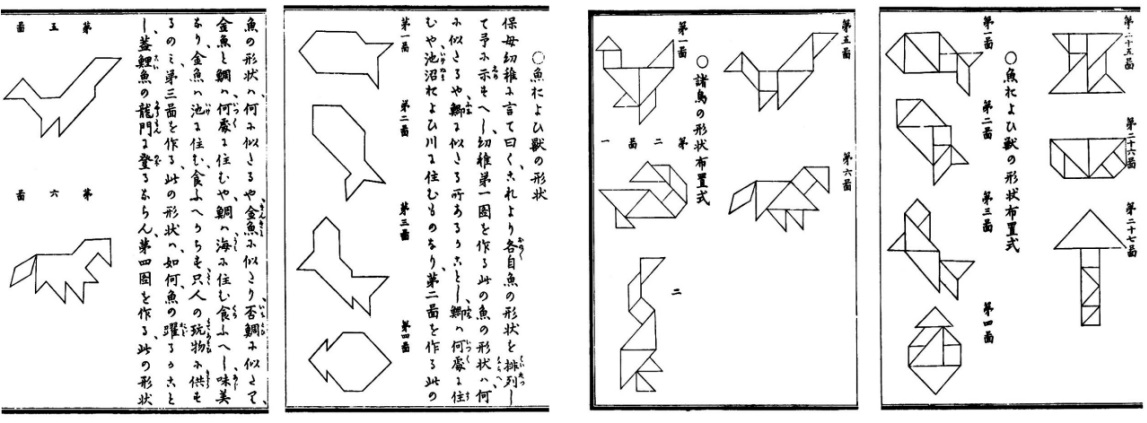
《幼稚智恵のみちひき》上卷（左）、下卷（右）
松浦政泰在明治40年（1907年）出版的《世界遊戲法大全》都有介紹七板的歷史和中國、西方的圖形，七巧板除了是玩具外，
也可作為數學敎育的輔助教具。
七巧板 – 《世界遊戲法大全》 松浦政泰 明治40年（1907年）
（左）十九枚智慧板和（右）益智圖（十五巧板） – 《世界遊戲法大全》 松浦政泰 明治40年（1907年）
昭和4年（1929年）藤五代策著東京培風館發行的《學校家庭手技及手工教材》第55至58頁〈板排〉和〈智慧板排〉
兩章節分別介紹「七巧板」和「清少納言智慧板」，亦繪列出幾款圖形。
〈板排〉和〈智慧板排〉–《學校家庭手技及手工教材》
勾
2 + 股
2 = 弦
2。
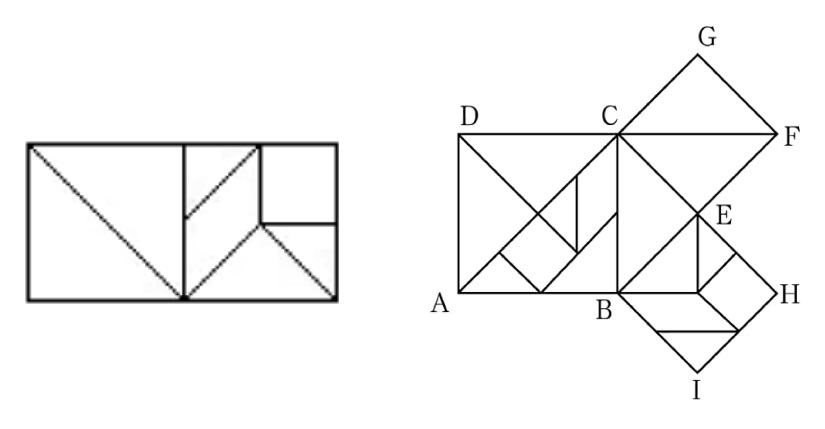
勾股定理
大家都知道七巧板成於四方形，也認識到如何拼出長方形和三角形，但「用一副七巧板能拼出多少個凸多邊形呢？」
這個數學問題由一位日本數學家於1930–40年代提出，中國浙江大學兩位學生王福春和熊全治（譯音）[2]
（Fu Traing Wang and Chuan-Chih Hsiung）於1942年用一個十分創新的方法，將這個幾何問題，用代數方法來解決。
他們的〈關於七巧板的一個定理（A Theorem on the Tangram）〉的證明文章刊於《美國數學月刊（The American Mathematical Monthly） 》
1942年第49卷第9號十一月刊第596–599頁，也收錄在《熊全治數學文選集（Selected Papers of Chuan-Chih Hsiung）》書
中（ 世界科學（ World Scientific ）出版 2001 第10–13頁）。著名的美國數學遊戲專家馬丁．加德納（Martin Gardner）
就稱讚他們的證明方法是有獨創性的。（見加德納的文章〈Concerning mechanical puzzles and how an enthusiast has collected 2000
of them〉–《科學美國人（Scientific American）》 1959年9月號 第238頁：「 Two mathematicians at the National University of
Chekiang - Fu Traing Wang and Chuan-Chih Hsiung published a paper in 1942 on just this problem.
Their approach was ingenious.」）
《科學美國人》 1959年9月號 第238頁
在討論王福春和熊全治的「關於七巧板的一個定理」的證明前，先要對七巧圖的分類有些少認識。
七巧圖中的各組塊只通過頂點與頂點或頂點與 邊相連接起來的，稱為非常規的七巧圖（Improper tangram）。
七巧圖中的各組塊是由 邊與邊相連接起來的， 稱為常規的七巧圖（Proper tangram）。拼成的圖形最多有23邊。
〈More on tangrams〉–《美國科學人》1974年9月號 p187–p191
非常規七巧圖(左)，常規七巧圖(右)，各有23邊
常規七巧圖中，有些是各組塊是經由有理邊（圖中小三角形的二邊為有理邊）與有理邊相連接、無理邊（圖中小三角形的斜邊是無理邊）
與無理邊相連接起來，且每條邊的邊段都要吻合相接，而且圖中無洞，羅納德．C．里德（Ronald C. Read） 稱之為正規七巧圖
（Regular tangram，里德稱之Snug tangram，見里德的書《Tangrams 330 Puzzles》）。
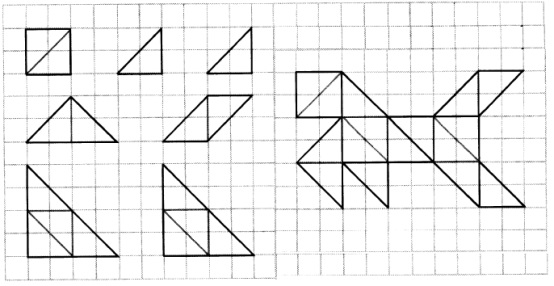
(左)七塊七巧板塊，(右) 正規七巧圖 – 有18條邊的小狗
一個平面閉合的圖形，如果在圖形內的任意兩點連成一直線而線上每一點都在圖形內，便是凸圖形；而在七巧圖上，只要圖上每一角都少於180°
，便是凸多邊形（Convex polygon）。
(左)凹圖形；(右)凸多邊形
這〈關於七巧板的一個定理〉文章裏的定理為︰
七巧板能做出的凸多邊形只有13個。
王福春和熊全治將七巧板看成由十六個小的等腰三角形構成，稱基本三角形，為方便證明起見，邊和斜邊分別稱為有理邊和無理邊，
然後證明多邊形的邊數不大於8，再討論凸多邊形可看成是內接於某矩形的情況，找出20個凸多邊形，其中只有13個是能用七巧板做出來。
在王福春和熊全治提出的文章證明中，沒有輔以圖形來說明。
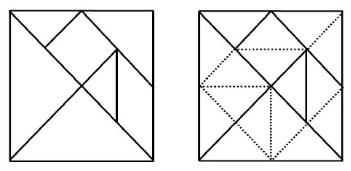
七巧板和16個基本三角形
在他們證明這定理前，先證明下述的引理：
| (i) |
若16個基本三角形組合成一個凸多邊形，則任一基本三角形的有理邊不會和另一基本三角形的無理邊重合。
|
| (ii) |
由16個基本三角形組成的凸多邊形，其每條邊要麽全是由基本三角形的有理邊組成，要麽全是由基本三角形的無理邊組成。
此外，如果把由基本三角形的有理邊組成的邊叫做凸多邊形的有理邊；把由基本三角形的無理邊組成的邊叫做凸多邊形的無理邊，
則一般而言，凸多邊形的有理邊和無理邊是交替出現的。只當凸多邊形的某個角是直角這種特殊情況下，
這個角的相鄰兩邊才要麽都是有理邊，要麽都是無理邊。
|
| (iii) |
由16個基本三角形組的凸多邊形，其邊數不超過8。
設凸多邊形的邊數是 n ，則其內角和是 (n - 2) π
因為由基本三角形合成的凸多邊形的內角，只能是 π/4，π/2 和 3π/4 ，所以
(n - 2) π ≤ (3π/4) n
因而 n ≤ 8
|
| (iv) |
如果16個基本三角形組成一凸多邊形，則該凸多邊形可內接於一個矩形，且該凸多邊形的所有有理邊或者所有無理邊就是該矩形的邊。
|
最後是證明定理。
我們可先假設這凸多邊形是個八邊形，由引理（ii）和引理（iv），這八邊形ABCDEFGH內接於矩形PQRS，其所有有理邊BC、DE、FG、HA 在矩形的邊
PQ、QR、RS、SP上。在AB、CD、EF、GH 邊上由 a、b、c、d 個基本三角形的無理邊做成；PQ 和QR 邊長分別與 x 和 y
個基本三角形的有理邊長一樣。
七巧板的面積是8 （因為基本三角形面積是1/2）。
於是有 1/2 a2 + 1/2 b2 + 1/2 c2 + 1/2 d2 = xy - 8
即 a2 + b2 + c2 + d2 = 2xy - 16
此外還有以下限制條件：
a + b ≤ x ， c + d ≤ x ， a + d ≤ y ， b + c ≤ y
然後找出適合這些條件的 a、b、c、d、x、y 的整數值。
大家可以參考王福春和熊全治〈關於七巧板的一個定理〉的證明，或參閱吳鶴齡著的《七巧板、九連環和華容道 – 中國古典智力遊戲三絕》一書，
在此就不詳述了。
王福春和熊全治總結這16個基本三角形可能做出的凸多邊形解答如下：
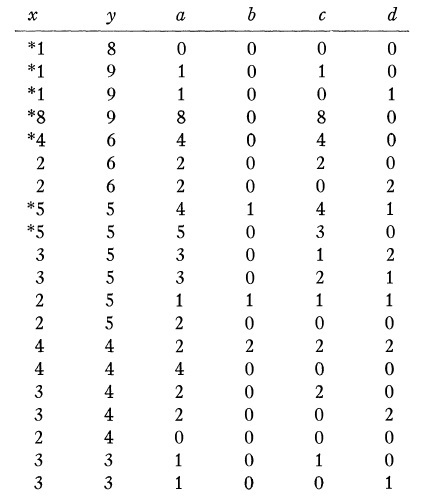
a、b、c、d、x、y 的整數值
表中所列而註有 * 的凸多邊形是不能用16基本三角形合成的七巧板做出來的，而其餘的13個就是可以由七巧板拼成的凸多邊形，
其中包括四個6邊形、兩個5邊形、六個4邊形和一個三角形，而每款凸多邊形可以有多於一種拼法。大家當然希望論文作者能夠給出這些圖形，
但很遺憾的是沒有。作者在文中說道：「但篇幅不允許把他們包括進來（but space does not permit their inclusion here ）。」
〈關於七巧板的一個定理 〉–《美國數學月刊 》1942年十一月
現在依據上面表列的數值，給出這13個凸多邊形如下，圖中括號內的數字是（ x y ： a b c d）之值。
能用七巧板拼成的13個凸多邊形
不能用七巧板拼出的凸多邊形如下：
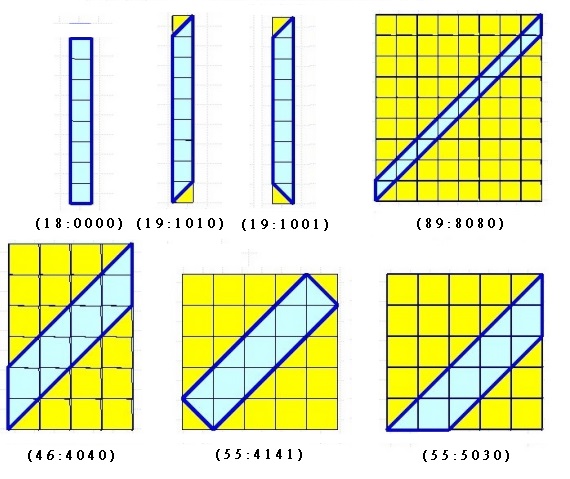
不能用七巧板拼出的凸多邊形
用七巧板能拼出的18個五邊形
其後多位讀者發現加納德的證明有些缺陷，並給出更多的圖形。1975年，東京的竹內（Dr. I. Takeuchi）博士用電腦程式確認有53個五邊形。
1976年，在沒有留意到竹內的工作下，美國馬薩諸塞州的邁克爾．比勒（Michael Beeler）也用電腦程式得到同樣結果，並把圖形繪出來，
加納德把比勒的結果放到他的《時間旅行和其他數學困惑（Time Travel and Other Mathematical Bewilderments） 》一書的一篇文章內。
用七巧板拼出53個五邊形
至於用清少納言智慧板能拼出多少個凸多邊形的問題，也可用王福春和熊全治的方法，得出可以拼出16個的結論。
用清少納言智慧板可以拼出16個凸多邊形
悖論的例子
下面的圖看來面積相等，但右面兩個卻多了空位。
另一悖論的例子
下面是清少納言智慧板的例子：圖左的一對看似一樣，但右側的圖形包含了一個空心三角形；圖右的一對很像，右側的卻有個三角形突出。
清少納言智慧板悖論例子
用兩套七巧板拼出的圖形例子解答
用三套七巧板拼出的圖形例子解答
伏羲女媧圖解答
益智圖解答
清少納言智慧板拼出的圖形例子解答
悖論的例子解答
另一悖論的例子解答
清少納言智慧板悖論例子
（二）各類型拼板
材料取自酒見康廣（Yasuhiro Sakemi）的文章〈「数学」におけるシルエットパズル教材の活用
（Effective Use of a Silhouette Puzzle in Teaching Mathematics）〉
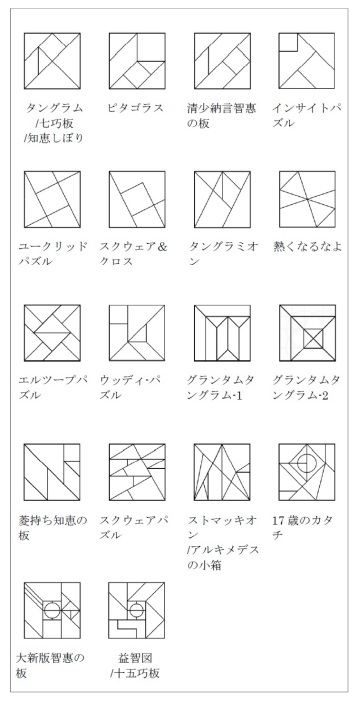
正方形型拼板謎
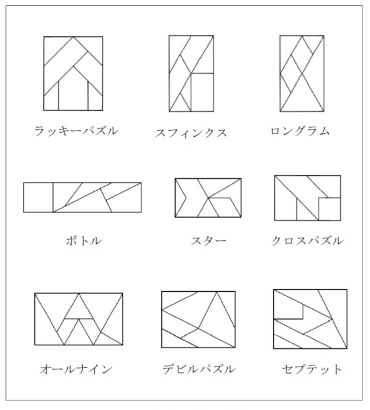
長方形型拼板謎
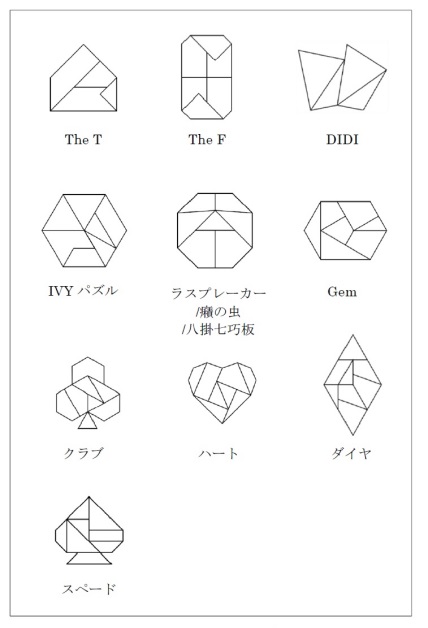
多角形型拼板謎
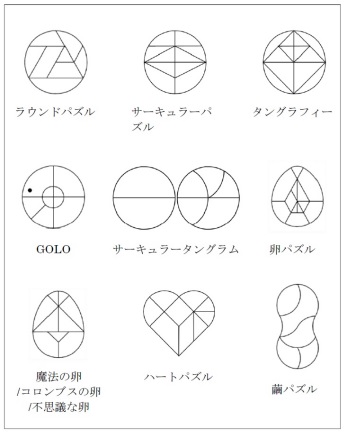
曲線形型拼板謎
【註】
| [1] |
因黄伯思卒于北宋徽宗初年，但《燕几圖》自序中說此書成於紹熙甲寅十二月丙午，即南宋光宗五年（公元1194年），
這並不符邏輯。如紹聖（北宋哲宗年號）誤作紹熙，則紹聖四年起於甲戌，盡於丁丑，其中並無甲寅年。往前算，
甲寅为北宋神宗熙寜七年；往後算，甲寅為南宋高宗紹興二十四年（應為紹興四年），都與黄伯思的生平無關。另外，伯思字長睿，
而《燕几圖》自序末題：「雲林居士黄長睿伯思序」這裏以字為名，以名為字，全部顛倒，難合常理，
也許是南宋人假托伯思大名而撰。然而，作者署名的問題並不影響《燕几圖》在家具史以及圖像文化史上的崇高地位。
見「從神奇的《燕几圖》看宋代的 “智者之變”」
（http://www.cncrafts.org/NewsShow.aspx?aid=951）。
〔宋代的幾次甲寅歳：熙寧七年（1074 甲寅）、紹興四年（1134 甲寅）、紹熙五年（1194 甲寅）〕
|
| [2] |
因為文章和作者名字都以英文書寫，所以只能音譯王福春和熊全治，亦有譯王福純和向全啓，不過在網上可找到王福春和熊全治的資料，
而且他們在1940年代都在浙江大學；卻沒有關於王福純和向全啓的。
|
參考資料
| （1） |
〈七巧板 – 會變化的平面〉–《有趣的數學遊戲》 林苑明譯 銀禾文化事業有限公司 1987年9月 p137–p148 |
| （2） |
〈七巧板〉、〈益智圖〉–《遊藝百寶箱》 朱育珉 江更生 湖南文藝出版社 1986年5月 p213–p262 |
| （3） |
第七章 〈七巧板之謎〉、第八章〈 益智盤〉–《奇妙數字遊戲》 高木茂男 文人譯 正業書局 民國67年1月（1978）
p77–p104 |
| （4） |
〈千姿百態七巧板〉–《七巧板、九連環和華容道 – 中國古典智力遊戲三絕》 吳鶴齡 科學出版社 2004 |
| （5） |
〈雞蛋遊戲(1)〉–《趣味智力遊戲全集》 余超群 武陵出版社 民國73年6月（1984） p117–p133 |
| （6） |
〈七巧與十五巧〉–《數學遊戲》 鄭肇楨 商務印書館 1980年9月 p153–p162 |
| （7） |
〈七巧與十五巧〉–《數學萬花筒 (1)遊戲篇》 九鼎出版社 民國75年3月（1986） p153–p162 |
| （8） |
〈拼板遊戲〉–《數學萬花筒 (3)奇幻篇》 九鼎出版社 民國75年3月（1986） p96–p104 |
| （9） |
第4章 第2節 〈七巧板〉–《東西數學物語》 〔日本〕平山諦著 代欽譯 上海教育出版社 p201–p207 |
| （10） |
〈清少納言知惠の板〉–《 雜藝叢書》 早川純三郎 國書刊行會 大正4年2月25日 （1915） p84–p.98
（ https://dl.ndl.go.jp/info:ndljp/pid/945792 ） |
| （11） |
〈清少納言知惠の板とタンダラム〉 高木茂男–《數學史研究》 通卷162號 1999年7–9月 p29–p41
（http://www.wasan.jp/sugakusipdf/162.pdf ） |
| （12） |
〈裁合物の事〉–《勘者御伽雙紙 上卷》 中根彥循著 中根 保之丞 法軸 編 天王寺屋市郎兵衛(京都) 寛保3年（1743）
p17–p25 （ https://dl.ndl.go.jp/info:ndljp/pid/3511864 ） |
| （13） |
〈複式知恵の板 〉–《世界遊戲法大全》 松浦政泰 博文館 明治40年12月（1907）
p83–p92 （ https://dl.ndl.go.jp/info:ndljp/pid/860315 ） |
| （14） |
〈「数学」におけるシルエットパズル教材の活用〉酒見康廣 中村學園大學短期大學部 研究紀要 第51號
2019年 p221–p225（ https://core.ac.uk/download/pdf/234605889.pdf ） |
| （15） |
〈シルエットパズルの凸配置の個數の研究〉 岩井仁志 北陸先端科學技術大學院大學 情報科學研究科 2016年12月
（ https://dspace.jaist.ac.jp/dspace/bitstream/10119/13839/5/paper.pdf ） |
| （16） |
〈A Theorem on the Tangram〉 Fu Traing Wang and Chuan-Chih Hsiung –《Selected Papers of Chuan-Chih Hsiung》
World Scientific 2001 p10–p13 |
| （17） |
〈A Theorem on the Tangram〉 Fu Traing Wang and Chuan-Chih Hsiung –《The American Mathematical Monthly》 Vol.49 No.9
（Nov., 1942） p596–p599 （ https://ur.booksc.me/book/48712381/ddfc60 ） |
| （18） |
〈Finding all convex tangrams〉 T. G. J. Beelen Eindhoven University of Technology（2017）
（ https://pure.tue.nl/ws/portalfiles/portal/54660270/casa17_02.pdf ） |
| （19） |
〈Notes on the Early History of the Tangram in Germany〉 Hartmut Walravens
（ https://cff.helm.lu/downloads/CFF72-Tangrams-Early-History.pdf ） |
| （20） |
〈Tangrams, Part 1〉, 〈Tangrams, Part 2〉–《Time Travel and Other Mathematical Bewilderments》 Martin Gardner
W.H. Freeman and Company 1988 p27–p54 |
| （21） |
〈Tangram Paradox〉–《Amusements in Mathematics》 H.E. Dudeney Dover Publications Inc. 1970 p43–p46 |
| （22） |
〈The Anchor puzzle〉 〈The Tormentor Puzzle〉 〈The Pythagoras puzzle〉 〈The Cross puzzle〉 〈The Circular puzzle〉,〈The Caricature puzzle〉,〈The Anchor puzzle Solutions〉 〈The Tormentor Puzzle Solutions〉 〈The Pythagoras puzzle Solutions〉 〈The Cross puzzle Solutions〉 〈The Circular puzzle Solutions〉,〈The Caricature puzzle Solutions〉–《Puzzles Old and New》 Professor Hoffmann London Frederick Warne and Co. 1893 p77–p87, p96–p97, p109–p121 , p128
（ https://ia800609.us.archive.org/19/items/puzzlesoldnew00hoff/puzzlesoldnew00hoff.pdf ） |
| （23） |
〈Models in plane geometry〉–《Mathematical Models》 H.M. Cundy and A.P. Rollett Oxford University Press Second Edition
1961 p19–p21 |
| （24） |
〈Tangram: The World's First Puzzle Craze〉 Jerry Slocum – 《A Lifetime of Puzzles》 Erik D. Demaine, Martin L. Demaine, Tom Rodgers A K Peters Ltd. 2008 p59–p76 |
| （25） |
〈Japanese Tangram: The Sei Shonagon Pieces〉 Shigeo Takagi – 《The Mathemagician and Pied Puzzler A Collection in Tribute to Martin Gardner》 Elwyn Berlekamp and Tom Rodgers CRC Press 2018 p97–p98 |
| （26） |
《七巧圖合璧》 碧梧居士 積書堂 嘉慶癸酉版 （日本天保十年） （1839）
（ http://www.wasan.jp/archive/sitikozu.pdf ） |
| （27） |
《七巧圖合璧》 碧梧居士 芳文閣 明治癸未版（日本明治十六年）（1883）
（ https://dl.ndl.go.jp/info:ndljp/pid/854421 ） |
| （28） |
《七巧八分圖（しちこうはちぶんず）》 秋芬室撰輯 商務印書館 1933年
（ https://kotenseki.nijl.ac.jp/biblio/100238922/viewer/1?ln=en ） |
| （29） |
《七巧新譜》 嘉慶丙子春月重鐫 （1816）《七巧圖解》 嘉慶丙子夏月新刊（1816） 聽雨樓珍玩
（ https://ia601200.us.archive.org/17/items/chichiaohsinpuch00unse_2/chichiaohsinpuch00unse_2.pdf） |
| （30） |
《益智燕几圖》・《益智圖》・《益智續圖》 童叶庚 平山文庫 1923年
（ https://kotenseki.nijl.ac.jp/biblio/100240014/viewer/1?ln=en ） |
| （31） |
《益智圖》 光緒戊寅（1878）版 藤原集書 同治元年（1862）
（ http://base1.nijl.ac.jp/iview/Frame.jsp?DB_ID=G0003917KTM&C_CODE=THKW-18142 ） |
| （32） |
《智恵乃いた （ちえのいた）》 新日本古典籍總合データベース
（ http://kotenseki.nijl.ac.jp/biblio/200018427/viewer/1 ） |
| （33） |
《教育遊戯七巧板》 奥沢信行 静黙居 日本明治28年2月（1895）
（ https://dl.ndl.go.jp/info:ndljp/pid/859909 ） |
| （34） |
《七巧板 – 中國古老的拼板遊戲》 約斯特‧埃爾費爾斯著 蔡錫明譯 北京出版社 1984年9月 |
| （35） |
《益智七巧圖》 R.J. 哈林岱爾著 蔡述彬譯 三越出版社 民國66年12月（1977） |
| （36） |
《七巧益智》 中華書局香港分局 1981年9月 |
| （37） |
《奇巧圖說 – 中國七巧文獻的奇葩》 梁紹傑、龍德義著 九章出版社 2006年9月 |
| （38） |
《The fashionable Chinese puzzle》 Ropes, John Codman 1859
（ https://archive.org/details/fashionablechine00rope/page/n23/mode/2up ） |
| （39） |
《The Chinese Boy and Girl》 Isaac Taylor Headland Fleming H. Revell Company The Caxton Press 1901 p116–p130
（ https://en.wikisource.org/wiki/The_Chinese_Boy_and_Girl ） |
| （40） |
《Tangram The Ancient Chinese Shapes Game》 Jooster Elffeers Penguin Books 1976 |
| （41） |
《Tangrams 330 Puzzles》 Ronald C. Read Dover Publications Inc. 1965 |
| （42） |
《Sam Loyd’s book of tangrams》 Sam Loyd Dover Publication Inc. 1968 |
| （43） |
江戸ちゑかた (江戶千方) 解答と問題の解說 （ http://www.chronos.co.jp/kenno/edo-chiekata.cgi ） |
| （44） |
清少納言知恵の板 問題の解說 （ http://www.chronos.co.jp/kenno/seisyonagon.html ） |
| （45） |
清少納言知恵の板（ https://www.puzzle-ch.com/chienoita/list.php?mode=&page=0 ） |
| （46） |
熊全治的自傳（ https://www.nandazhan.com/xueshu/lquanzhi.htm ） |
| （47） |
王福春（民國時浙江大學數學系教授）
（https://baike.baidu.hk/item/%E7%8E%8B%E7%A6%8F%E6%98%A5/63672）
|
| （48） |
平山諦（ https://ja.wikipedia.org/wiki/%E5%B9%B3%E5%B1%B1%E8%AB%A6 ） |
木製七巧板
七巧板的板塊做法
用一套七巧板拼出的圖形例子
用兩套七巧板拼出的圖形例子
用三套七巧板拼出的圖形例子
《欽定續文獻通考》卷一百八十一〈經籍考〉四十一 頁三十三
《欽定四庫全書總目》卷一百十六子部譜錄類存目 頁十一至十二
《海虞藝文志》卷五第二頁
《燕几圖》 黃長睿撰
（《叢書集成初編燕几圖及其他四種》王雲五主編 商務印書館 民國二十五年十二月（1936））
《蝶几譜》
《中國之科學與文明》 第三卷
清劉獻廷筆記《廣陽雜記》卷三
「七巧圖」 –《冷廬雜識》 卷一 咸豐六年丙辰（1856年）
《七巧圖合璧》 桑下客序 芳文閣出版 明治16年（1883年）
《七巧新譜》桑下客序 清道光癸未春月重鎸（1823年） 春雨樓珍玩 福文堂藏板
《七巧圖合璧》嘉慶18 年癸酉 （1813年）
《七巧圖合璧》 道光13年癸巳（1833年）
（左）《七巧新譜》一頁，（右）《七巧圖解》給的解答 嘉慶丙子 (1816年)
（左）《七巧新譜》一頁，（右）《七巧圖解》給的解答 道光癸未（1823年）
《七巧新譜》山樵自序 嘉慶二十一年(丙子 1816年) 聽雨樓
《彚增七巧圖》卷尾解說
《以當一瓻》 裘良白自序
《以當一瓻》書中部份圖式
《七巧八分圖》序 –王其沅 秋芬室撰輯 商務印書館（1933年重版，1918年初版）
《七巧八分圖》內頁（左）編輯資料及圖形 （右）王念慈為母錢芸吉寫的題誌
《七巧八分圖補遺》序 – 王其沅（錢芸吉夫） 秋芬室撰輯 商務印書館 （1933）
《七巧書譜》跋 聽月山房
《七巧書譜》圖式
《信手拈來》序及圖式 清光緒二十七年（1901年） 馮氏德聚堂刻本
《中英字母七巧圖》連仰山 自序
《中英字母七巧圖》圖形 連仰山 民國二十二年（1933年）第一版
《益智圖》上卷–巢睫山人小影
《益智圖》– 十五巧板
《益智圖》序 – 廣陵沁庵氏
《益智圖》自序 – 巢睫山人
《睫巢鏡影》秦跋 光緒十六年庚寅（1890年）
《益智圖千字文》– 恭親王的題字「操觚新格」
《益字圖千字文》跋 – 巢睫散人
益智圖 – 故宮博物院藏
《益智圖》
《益智續圖》
《益智燕几圖》
《益智燕几圖副本》 商務印書館 1933年國難後第一版
《益智燕几圖副本》跋 – 祝梅君
《益智字圖》 – 祝梅君
《益字圖千字文》
《益智圖千字文》及《智永真書千字文》節字對比
廣告：益智圖千字文商務印書館發行 東方雜誌 第十六卷 第一號 (1919年)
「天然巧合」 吳友如 （1892年）
《趙太史竹岡齋九種》–《 竹岡雜綴續 》第四十九頁的〈七巧圖序〉 （1816年）
〈題七巧圖〉 《古藤書屋詩鈔》– 錦江集 同治六年丁卯 （1867年）
《餘墨偶談》卷七續集的〈七巧圖〉光緒二年丙子（1876年）
「詩情畫意册序」《 荻芬書屋文稾 》序 第四十頁（1876年）
圖左是古畫〈伏羲女媧圖〉，圖右是由兩副七巧板拼成的〈伏羲女媧圖〉
《時尚中國謎題》
在美國和英國售賣七巧板和書的廣告
《法國新拼板遊戲》其中一頁
早期意大利書《新中國遊戲）》弗蘭澤特（Franzetti）1817年
七巧板是家庭趣味解題遊戲 – 1820年
洛伊德《唐第八卷書之第一部》
洛伊德《唐第八卷書之第一部》其中一頁
洛伊德的《七巧圖（The Tangram Book）》斯坎頓公司（Scanton Life Ins. Co.） 1917
杜德尼在《河濱雜誌》的文章
《唐第八卷書之第一部》 1969年1月1日版
《數學公報》介紹伊洛德的《唐第八卷書之第一部》
《第二輯數學謎題》書中〈機械拼圖〉章（ p210–p214）
《科學美國人》1974年8月號
《美國教育雜誌》1859年 3月–6月號 VolVI_NoXVI - NoXVII p452
《伊利諾伊州教師》1864年8月號卷10
《弗里曼雜誌（Freeman's Journal）》 19 June 1817 中推銷七巧板的廣告
《柏林報紙（Berlinische Zeitung）》1822年 七巧圖廣告
