折紙手藝 兒童摺紙 組合摺紙 恐龍摺紙 中國龍摺紙 摺紙盒子 摺紙蛇 摺紙馬 聖誕摺紙 立體鬆鬆摺紙 摺紙龜 摺紙龍舟 鬆鬆摺紙 虎年摺紙 摺紙索馬立方體 摺紙七巧板

組合摺紙               　　　 　　　      〈一〉 組合摺紙      〈二〉 我的經驗      〈三〉 幾何立體模型      〈四〉 單元件的摺法      〈五〉 做個立體星      〈六〉 摺紙示例      〈七〉 相關書籍       <一> 組合摺紙 根據 David Mitchell 定義，組合折紙是一種包含對多張紙作兩個程序的折紙技巧。第一個程序是將每一張紙都折成相同的模單元，然後第二個程是將各模單元組合成平面或立體的結構。由一組相同模單元組合成的是正規組合折紙，多數的組合折紙均屬此類。亦有由多組不同模單元合成的，謂不正規組合折紙。有關這方面的資料，請參閱David Mitchell 網址： http://freespace.virgin.net/dave.mitchell/modularorigamiindex.htm 最早的組合折紙相信是一種名為 Tematebako 的設計，源於 1734 年或更早的時候。直到六十年代再由美國人 Robert Neale 獨立發明出來，然後是日本人 Mitsonobu Sonobe 對此亦大有頁獻。日本資深紙藝家笠原邦彥〈Kunihiko Kasahara〉亦是長於此道，但組合折紙仍未流行。及至布施知子〈Tomoko Fuse〉推出她在這方面的大量作品，才把組合折紙發揚光大。 回返   　　　   <二>  我的經驗 我對組合折紙的興趣，始於九十年代初，源於一套從日文折紙世界翻譯成中文的台灣折紙書，其中布施知子的《立體造型折紙》、《長方形折紙》和《立體的秘密》，我特別喜愛，其立體幾何模型的作品，我都一個一個嘗試的去摺。 摺組合折紙的單元件，一般並不太難，不過每一單元件都要按步驟盡量摺得準確，縮少誤差，否則製成的多面體會歪歪斜斜的。在將各單元件組合時會有些難度，尤其是在安裝最後幾個單元件時，要用些少技巧。理論上組合折紙不用膠水黏合，這增加了組合時的困難程度，而且製成品不易保持。因此我會在組合的過程中，用少許白膠漿把單元件黏合，這可克服製品在組合過程中容易破散的情況，而製成品在完成後表現得十分挺硬，不易變型。           立體造型折紙   長方形折紙   立體的秘密     回返   　　　   <三> 幾何立體模型 組合折紙多用於組合幾何立體模型，如柏拉圖立體 (Platonic solids)、阿基米德立體(Archimedean Solid)、開普勒星形正多面體(Kepler-Poinsot polyhedra)、截頂多面體(Truncated polyhedra) 、巴克球(Buckyball)等等，其基本骨架都是從柏拉圖立體的骨架而來。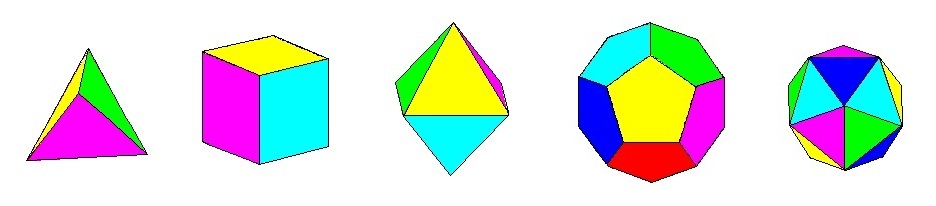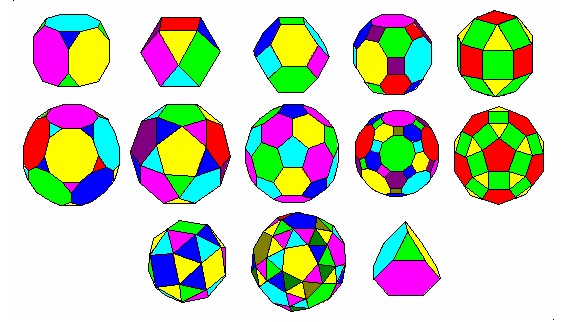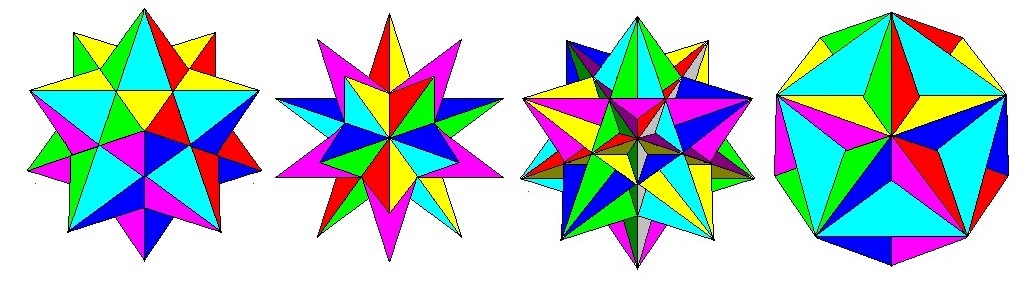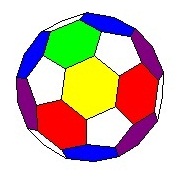 柏拉圖立體   阿基米德立體   開普勒星形正多面體   巴克球 – 32 面(20個六邊形12個五邊形)   多面體摺紙可由 2 – 240 不同單元件組合而成，單元件數目不能隨意增減，而且要按一定規則去組合。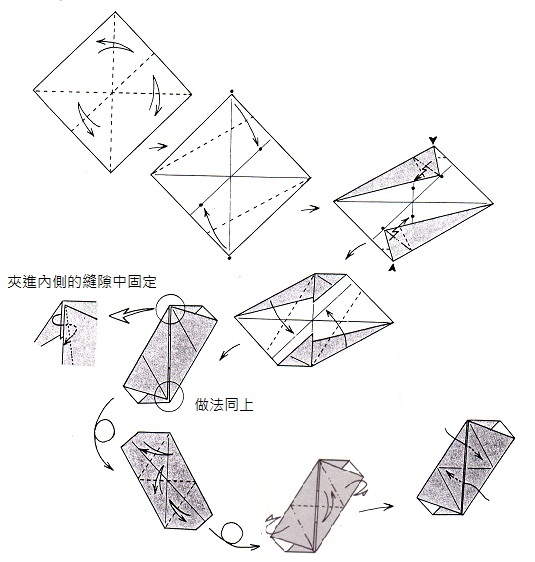   　　　           四面體-由2 個正逆單元件組成   正立方體-由六個單元件組成   C240 巴克球-由240 個單元件組成       回返   　　　 　　　   <四>  單元件的摺法 單元件的摺法有多種，最簡單的是由日本人Mitsonobu Sonobe 所發明的Sonobe 單元件。   Sonobe 單元件摺法   用六個Sonobe 單元件，可以組成一個正六面體。 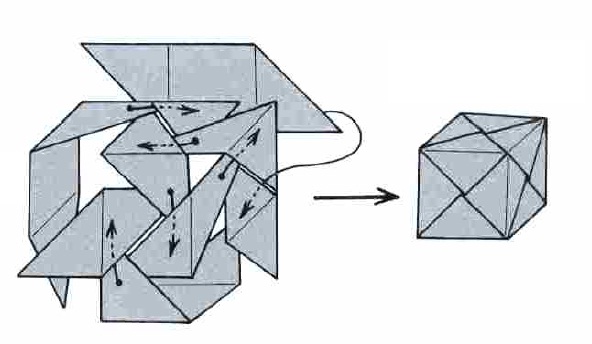正六面體   若將Sonobe 單元件在摺法上加以小小變化，製成的立體更加美麗。 　　　 　　　 　　　       回返   　　　   <五> 做個立體星 下面介紹的立體，是布施知子的作品。 請預備30張方形紙，依下圖所示，摺30個相同單元件。 這立體星按20面體的骨架組合而成。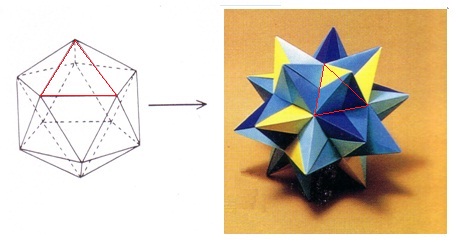 每一星角由三個單元件合成。 在摺過立體星後，大家可以利用前面的柏拉圖立體、阿基米德立體、開普勒星形正多面體和巴克球，或參考下面的多面體骨架，依著剛獲得的經驗，嘗試向難度挑戰吧！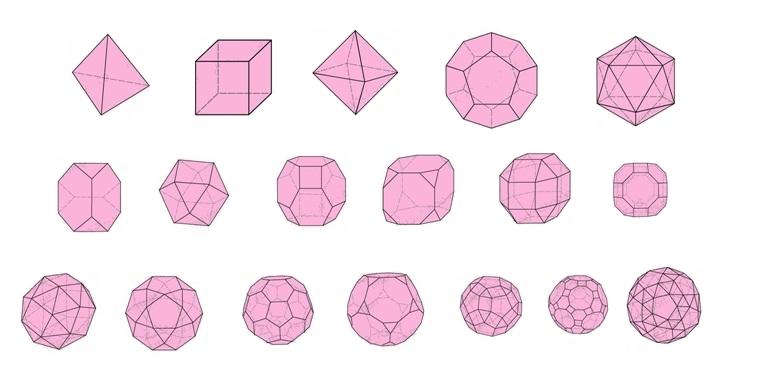   回返   　　　   <六> 摺紙示例   回返         <七> 相關書籍             立體折紙   趣味摺紙百科   長方形折紙   立體造型折紙         Modular Origami   Multimodular   Origami   Polyhedron Origami Polyhedra   Origami Polyhedra       for Beginners         Unit Origami   Unit Polyhedron   立体をっくろう   立体からくり     Origami                         回返       © 2010 KT LI

摺紙學會網站   香港摺紙社   澳洲伯斯摺紙組   英國摺紙學會   美國摺紙學會 推薦網站 Robert J. Lang Origami Origami Mathematics